Нечеткие множества в хранилище данных
Автор: Потапов Евгений Николаевич
31 Мая 2011 г.
История нечетких множеств
Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество - понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1.
С конца 80-х годов и до сих пор идет бумом практического применения теории нечеткой логики в разных сферах науки и техники. До 90-ого года появилось около 40 патентов, относящихся к нечеткой логике. Сорок восемь японских компаний создают лабораторию LIFE (Laboratory for International Fuzzy Engineering), японское правительство финансирует 5-летнюю программу по нечеткой логике, которая включает 19 разных проектов — от систем оценки глобального загрязнения атмосферы и предвидения землетрясений до АСУ заводских цехов. Результатом выполнения этой программы было появление целого ряда новых массовых микрочипов, базирующихся на нечеткой логике. Сегодня их можно найти в стиральных машинах и видеокамерах, цехах заводов и моторных отсеках автомобилей, в системах управления складскими роботами и боевыми вертолетами. В США развитие нечеткой логики идет по пути создания систем для большого бизнеса и военных. Нечеткая логика применяется при анализе новых рынков, биржевой игре, оценки политических рейтингов, выборе оптимальной ценовой стратегии и т.п. Появились и коммерческие системы массового применения.
Описание
Характеристикой нечеткого множества выступает функция принадлежности (membership function). Обозначим через µ(x) степень принадлежности элемента x к нечеткому множеству, представляющую собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C = {µ(x)/x}, при этом µ(x) может принимать любые значения в интервале [0, 1]. Значение µ(x) = 0 означает отсутствие принадлежности к множеству, 1 — полную принадлежность.
Проиллюстрируем это на простом примере. Формализуем неточное определение «неблагонадежный заемщик». В качестве X (область рассуждений) будет выступать количество случаев просроченной задолженности по кредиту за последние 6 месяцев. Пусть оно изменяется от 0 до 6. Нечеткое множество, определенное экспертом, может выглядеть следующим образом:
C = {0/0; 0,4/1; 0,7/2; 0,9/3; 1/4; 1/5; 1/6}.
Так, заемщик, совершивший две просрочки, принадлежит к множеству «неблагонадежный» со степенью принадлежности 0,7. Для одного банка такое число просрочек может быть крайне существенным, для другого — просто тревожным сигналом. Именно в этом и проявляется нечеткость задания соответствующего множества.
Для переменных, относящихся к непрерывному виду данных, функцию принадлежности удобнее задать аналитической формулой и для наглядности изобразить графически. Существует свыше десятка типовых форм кривых для задания функций принадлежности. Рассмотрим самые популярные кусочно-линейные: треугольную и трапецеидальную.
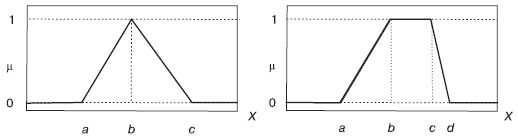
Рис. 1. Типовые функции принадлежности
Треугольная функция принадлежности определяется тройкой чисел (a, b, c), и ее значение в точке x вычисляется согласно выражению:
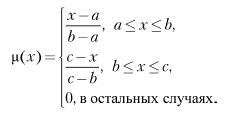
Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a, b, c, d):
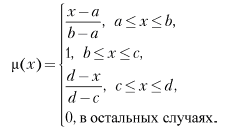
Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми необходимыми для расчетов являются пересечение, объединение и отрицание.
Для нечетких множеств можно применить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значение mA(x), на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами.
Пусть A нечеткий интервал между 5 до 8 и B нечеткое число около 4, как показано на рисунке.
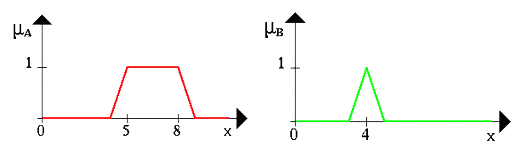
- Пересечение двух нечетких множеств A ∩ B (нечеткое «И»):
µ(x) = min(µA(x), µB(x)).
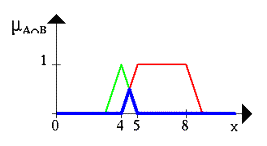
Рис.2. Нечеткое множество между 5 и 8 И (AND) около 4 (синяя линия)
- Объединение двух нечетких множеств A ∪ B (нечеткое «ИЛИ»):
µ(x) = max(µA(x), µB(x)).
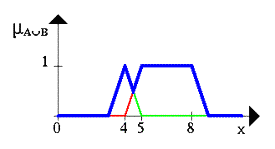
Рис.3. Нечеткое множество между 5 и 8 ИЛИ (OR) около 4 показано на следующем рисунке (снова синяя линия).
- Отрицание нечеткого множества -A:
µ(x) = 1 - µA(x),
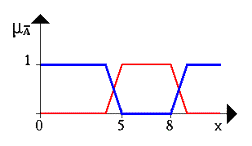
Рис.4. Операцию отрицания. Синяя линия — это ОТРИЦАНИЕ нечеткого множества A.
где
µ(x) — результат операции;
µA(x) — степень принадлежности элемента x к множеству A;
µB(x) — степень принадлежности элемента x к множеству B.
Совокупность нечетких множеств, относящихся к одному объекту, образует лингвистическую переменную. Например, лингвистическая переменная Возраст может принимать значения Молодой, Средний, Пожилой (их еще называют базовым терм-множеством, или термами). Зададим область рассуждений в виде X = {x | 0 < x < 90} (годы). Теперь осталось построить функции принадлежности для каждого терма (рис. 5).
Каждая функция принадлежности описывается четверкой чисел: Молодой = {0; 0; 12; 40}, Средний = {20; 30; 50; 70}, Преклонный = {50; 60; 90; 90}.
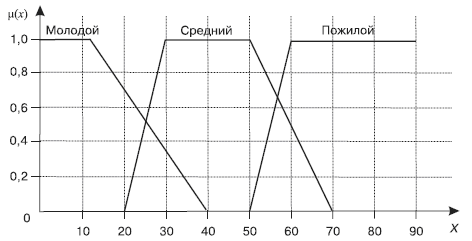
Рис. 5. Графическое изображение лингвистической переменной «Возраст»
Нечеткий поиск в хранилище данных
Лингвистические переменные можно задать для любого измерения, атрибута измерения или факта, значения которого имеют непрерывный вид. Их параметры: названия, терм-множества, параметры функций принадлежности — будут содержаться в семантическом слое хранилища данных (рис. 6).
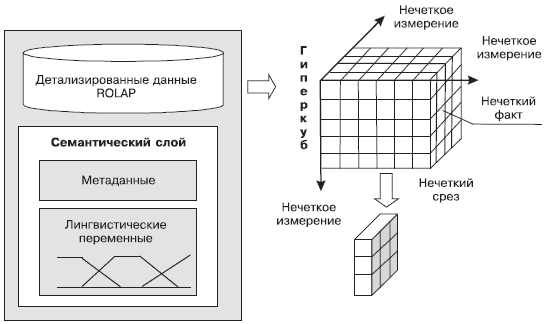
Рис. 6. Вариант организации хранилища данных с поддержкой нечетких срезов
Результатом выполнения нечеткого среза, помимо самого подмножества ячеек гиперкуба, удовлетворяющих заданным условиям, является индекс соответствия срезу CI [0, 1]. Он представляет собой итоговую степень принадлежности к нечетким множествам измерений и фактов, участвующих в сечении куба, и рассчитывается для каждой записи набора данных. Чтобы ускорить выполнение запросов к ХД, часто задают верхнюю границу индекса соответствия CI > а. Это позволяет уже на уровне SQL-запроса отсеять записи, которые заведомо не будут удовлетворять минимальному порогу индекса соответствия (рис. 7). На рисунке видно, что элементы нечеткого множества со значениями в интервале [xf, x2] обеспечат степень принадлежности не ниже а.
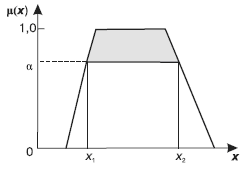
Рис. 7. Нечеткое множество
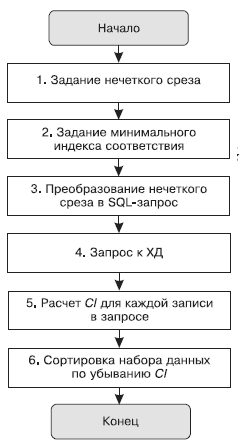
Рис. 8. Алгоритм получения нечеткого среза
Алгоритм формирования нечеткого среза иллюстрирует схема (рис. 8). На шаге 1 используется семантический слой хранилища данных. На шаге 3 в результирующий SQL-запрос попадают границы с учетом минимального индекса соответствия а. Шаг 5 предполагает применение нечетких логических операций pouvez trouver ici.
Рассмотрим пример. Пусть в хранилище содержится информация о соискателях вакансий, и срез (четкий) по измерениям Код анкеты, Возраст и Стаж работы обеспечивает следующий набор данных (табл. 1).
Очевидно, что Код анкеты — это служебное поле. Для возраста будем использовать лингвистическую переменную, определенную на рис. 5, а для поля Стаж работы — переменную, определенную на рис. 9. Каждая функция принадлежности описывается числами: Малый = {0; 0; 6}, Продолжительный = {3; 6; 10; 20}, Большой = {15; 25; 40; 40}.
Таблица 1. Срез по измерениям «Возраст» и «Стаж работы»
| Код анкеты | Возраст | Стаж работы |
|---|---|---|
| 1 | 23 | 4 |
| 2 | 34 | 11 |
| 2 | 34 | 11 |
| 3 | 31 | 10 |
| 4 | 54 | 36 |
| 5 | 46 | 26 |
| 6 | 38 | 15 |
| 7 | 21 | 1 |
| 8 | 23 | 2 |
| 9 | 30 | 8 |
| 10 | 30 | 12 |

Рис. 9. Графическое изображение лингвистической переменной «Стаж работы»
Сделаем нечеткий срез «Возраст = Средний и Стаж работы = Продолжительный». Например, для анкеты 4 получим:

Аналогично рассчитаем степени принадлежности к итоговому нечеткому множеству для каждого претендента, зададим минимальный индекс соответствия, равный 0,3, и получим результат, показанный в табл. 2.
Таблица 2. Результат нечеткого среза
| Код анкеты | Возраст | Стаж работы | Индекс соответствия |
|---|---|---|---|
| 3 | 31 | 10 | 1 |
| 9 | 30 | 8 | 1 |
| 6 | 38 | 15 | 1 |
| 2 | 34 | 11 | 0,9 |
| 10 | 30 | 12 | 0,8 |
| 8 | 23 | 2 | 0,3 |
| 1 | 23 | 4 | 0,3 |
Нечеткий поиск в хранилищах данных принесет аналитику максимальную пользу в случаях, когда требуется не только извлечь информацию, оперируя нечеткими понятиями, но и каким-то образом проранжировать ее по убыванию (возрастанию) степени релевантности запроса. Это позволит ответить на следующие вопросы: каких клиентов обзвонить в первую очередь, кому сделать рекламное предложение и т.д.
Источники:
[1] книга «Бизнес-аналитика: от данных к знаниям» Орешков В.И., Паклин Н.Б.
[2] Википедия
[3] Теория логики